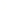This article is part 4 of a 5 part series introducing the core concepts of Intonal. It assumes a basic knowledge of music and terms MIDI, tempo, synthesizer, and lowpass filter. It assumes no prior programming knowledge, and is written for all audiences new to Intonal.

Over the previous tutorials we've glossed over an important subject - how do streams advance? Initially you may think that each stream is advanced for each tick of the main transform, however the fby ... on structure (what we've been using to slow an array to change at the tempo) introduced in tutorial 2 clearly doesn't work that way.
The rule behind this implicit advancing is simple - if a stream is referenced one or more times then it is advanced once. Take for example the if statement:
The guiding principal behind Intonal's control flow design is that the consumer/user of a stream should have control over how the stream is advanced. That's what lets us, in the previous two tutorials, take a stream of notes and slow it down to the speed of the tempo.
In this tutorial we'll build a rough NES emulator using two square waves and a triangle wave. We'll look at four different approaches to synthesizing these waveforms.
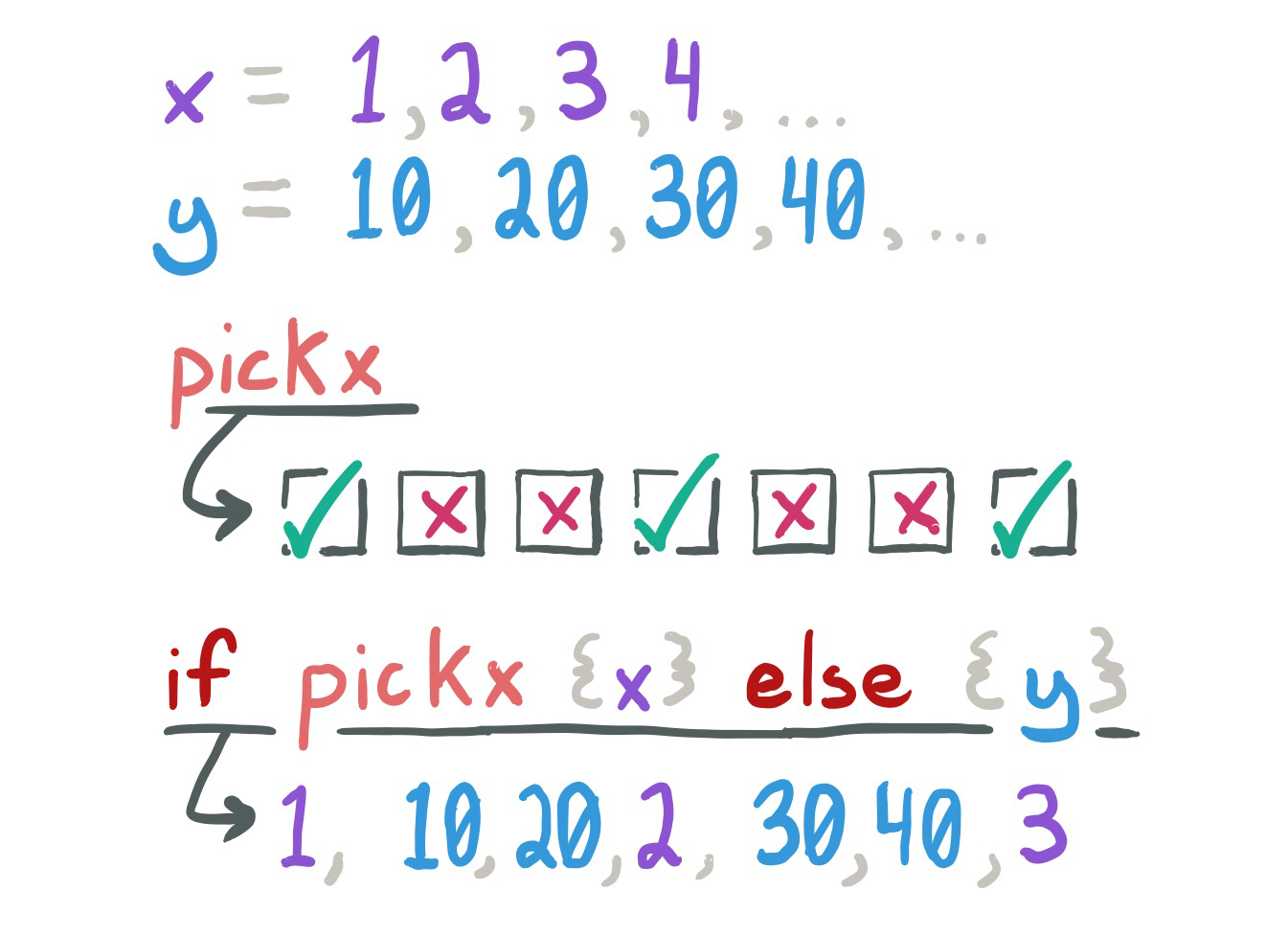
The naive approach is to use phasor to build a simple square wave and triangle wave. Set synthesisType to naiveSynthesis in the example to hear the result.
squareWave = {hz: float32, sr: float32 in
p = phasor(hz, sr)
out = if p < 0.5 {-1} else {1}
}
triangleWave = {hz: float32, sr: float32 in
p = phasor(hz, sr)
out = if p < 0.5 {p * 4 - 1} else {1 - ((p - 0.5) * 4)}
}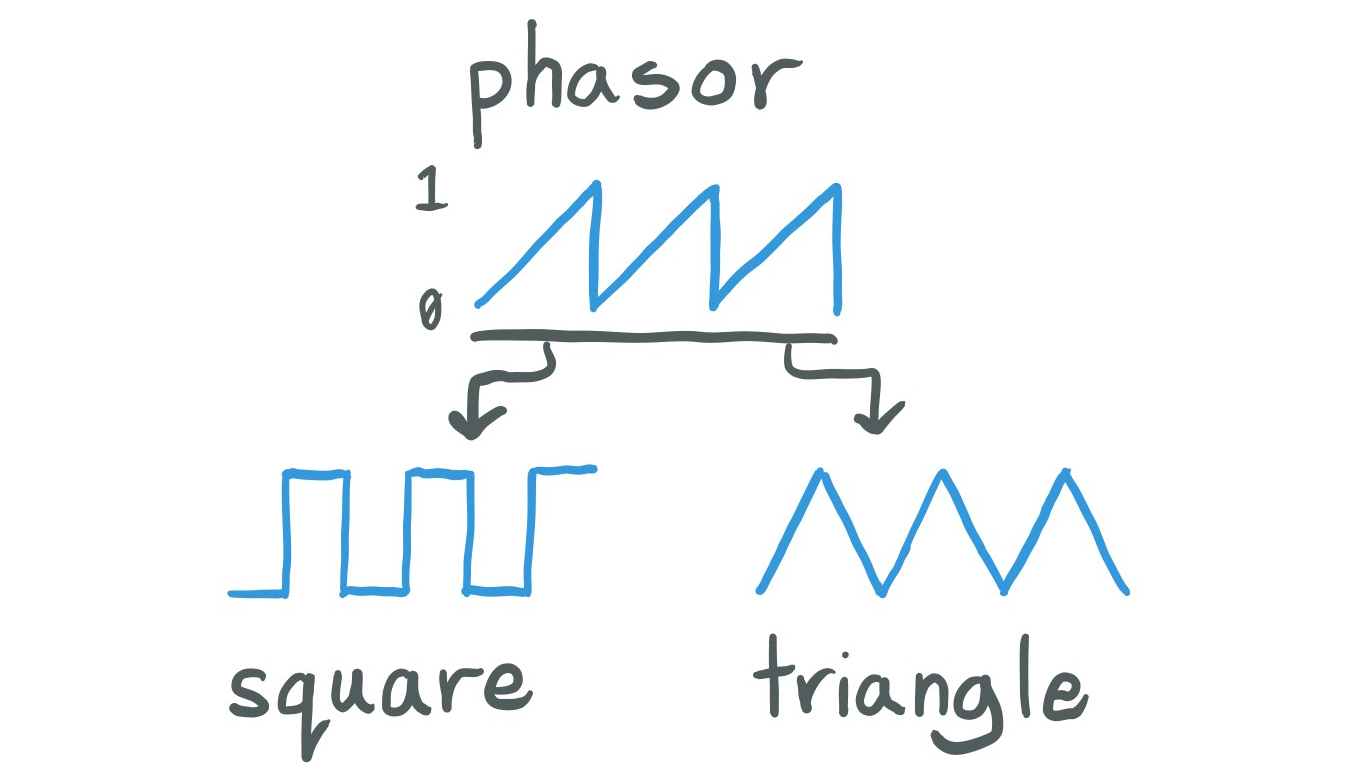
You may notice a harsh buzzing in this version. This is a side effect of our sampling rate.
The faster the sampling rate, the higher frequencies we can play back. To be precise we can recreate frequencies up to half the sampling rate - also known as the Nyquist Frequency. But what happens when you attempt to play back a frequency higher than the Nyquist? The higher frequencies don't just disappear, they wrap around the Nyquist, causing the harsh inharmonic buzzing in our naive synthesis above. This effect is called aliasing.
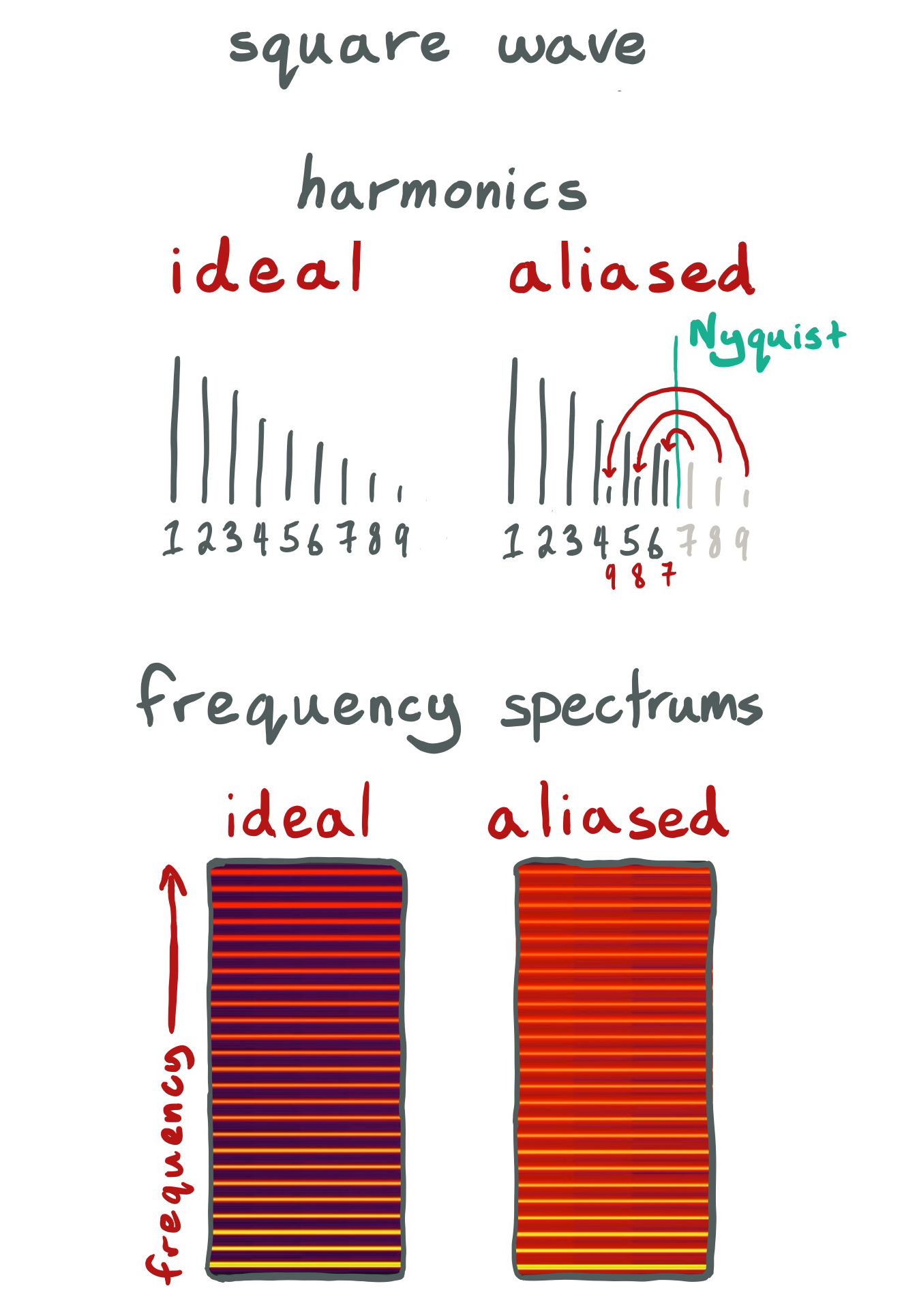
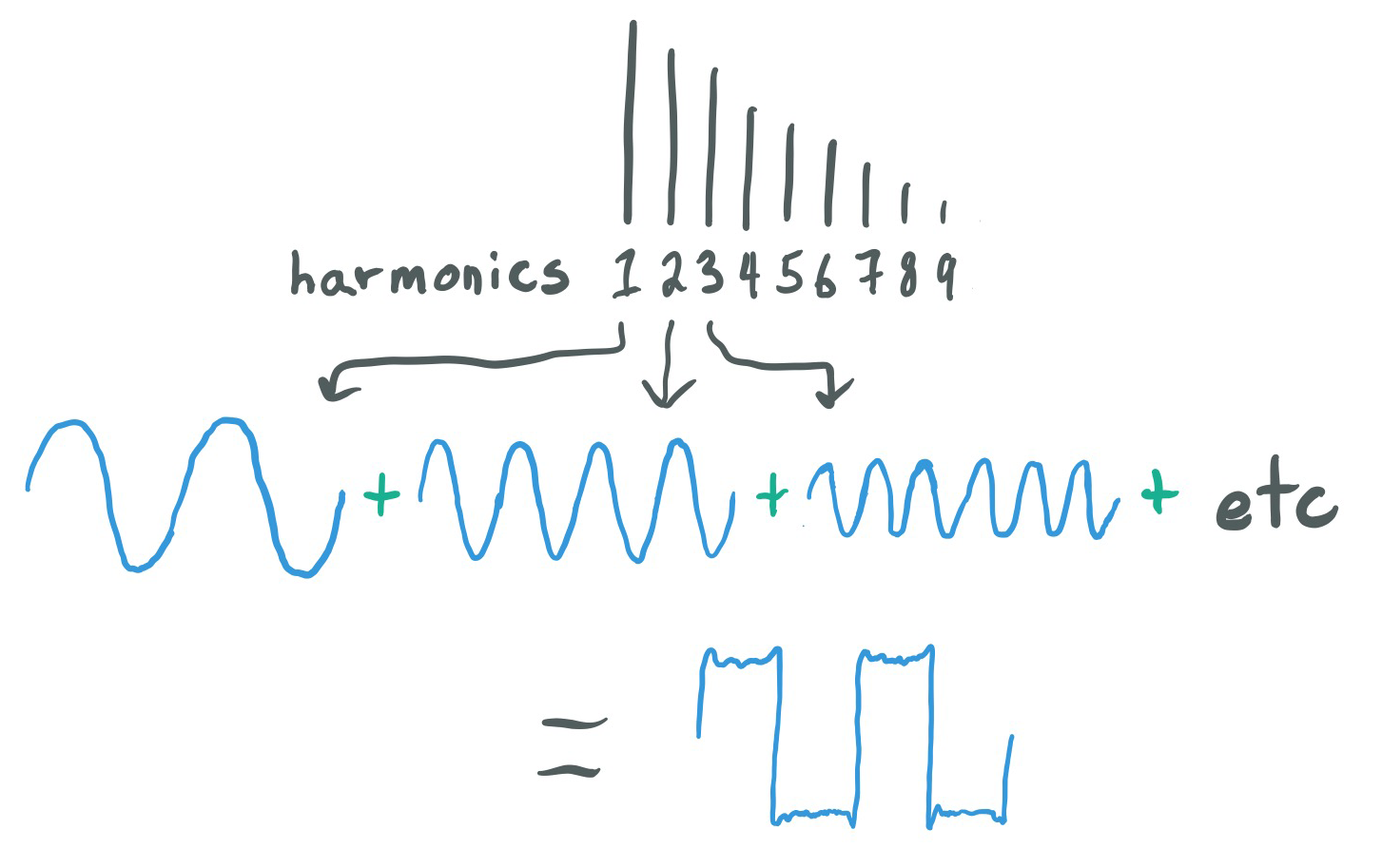
To produce anti-aliased square and triangle waves we can build them from their individual harmonics. This technique is called additive synthesis.
There's a simple equation for the harmonics of a square wave, so we can build a band-limited (limiting the frequency bands within an acceptable range) version of a square wave. Here's the formula for the amplitudes of a square wave:
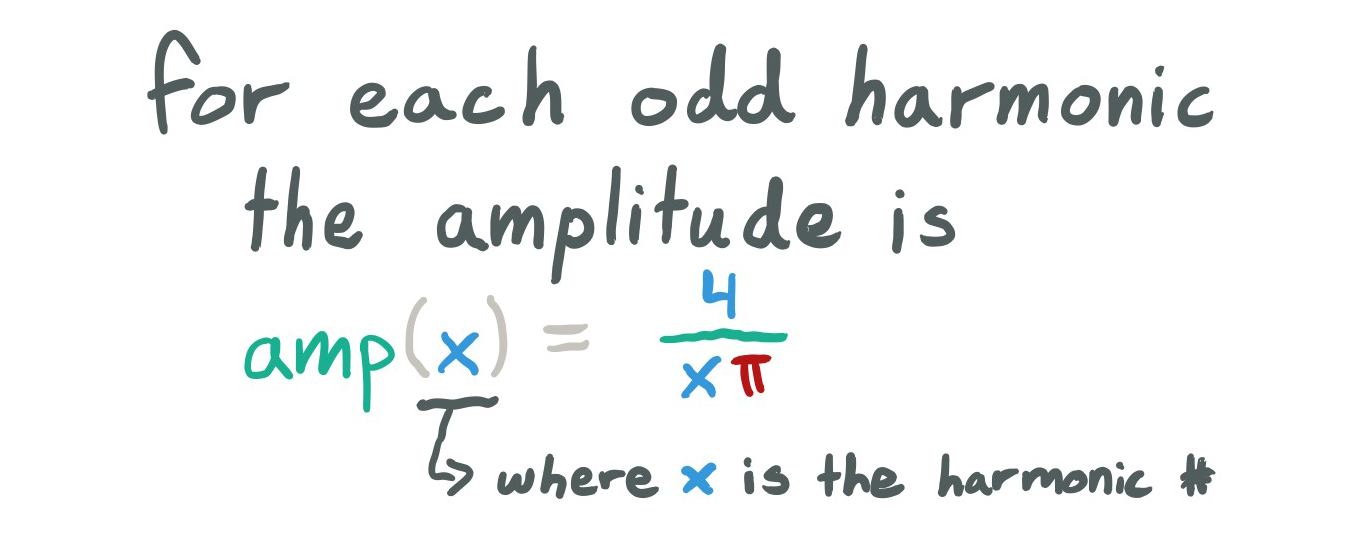
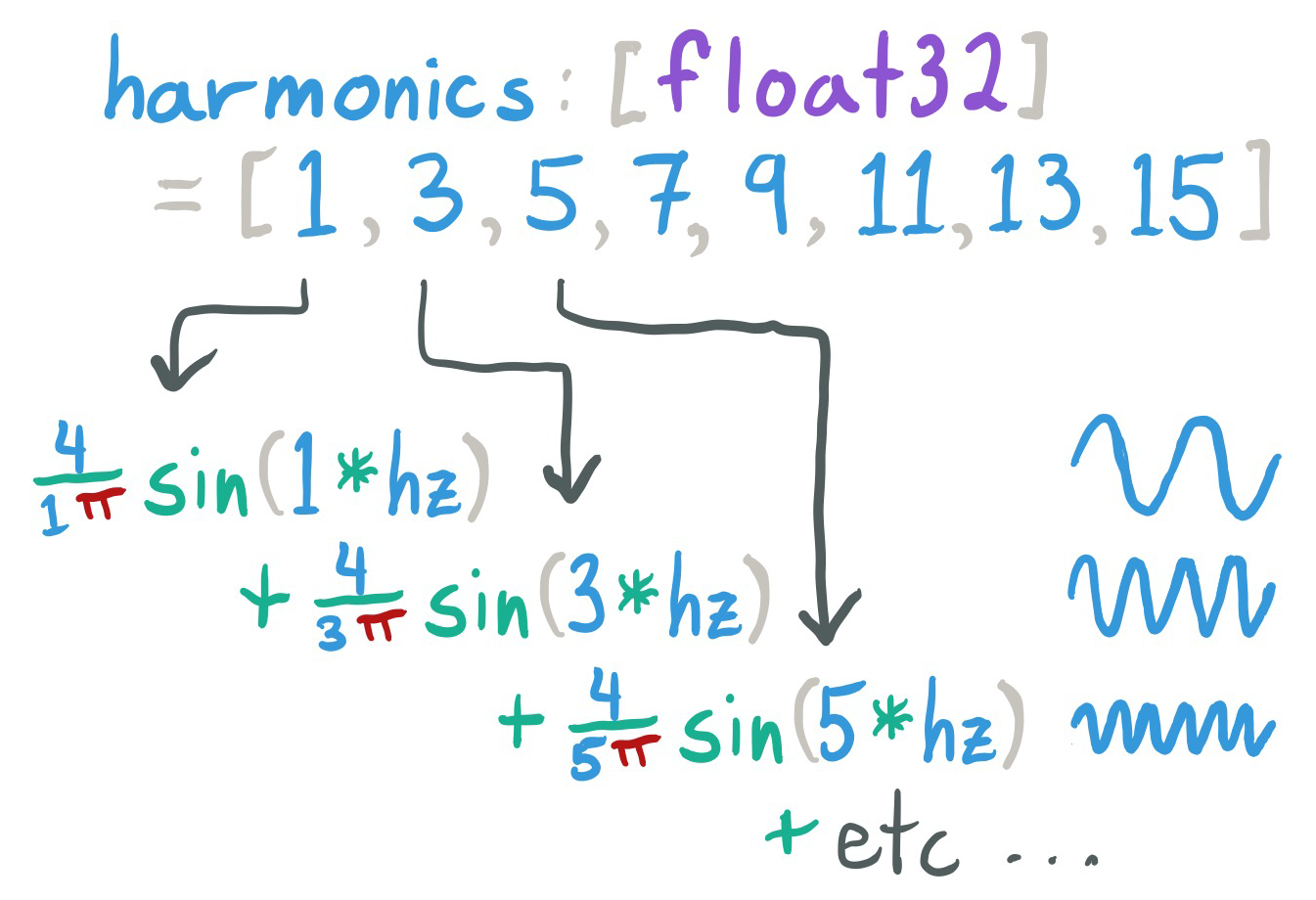
To handle an arbitrary number of harmonics, we need to build an array of the harmonics we want and then convert each of those to a sine wave.
But how do we build an array of an arbitrary number? We need something that's the inverse of streamify - where streamify takes an array and produces a stream from the arrays values, we want to take a stream and produce an array. For this we use the built-in transform render.

While if and fby ... on allow slowing down streams, render is used to speed up streams. Since we only want the start of the stream we use on init to "freeze" the stream, only running the render once.
To convert the array of harmonic numbers to sine waves, we use multiReduce, which is very similar to the map we looked at in an earlier example, except that it produces a single value rather than a new array. Here is a good break down of the difference between map and reduce.
Set synthesisType to additiveSynthesis in the example to hear the result.
// Band-Limited Square Wave
makeBlAdditiveSquareWave = {numHarmonics: uint64 in
out = {hz: float32, sr: float32 in
curHarmonic: float32 = 1 fby prev + 1
harmonics = render(2 * curHarmonic - 1, numHarmonics) on init
out = harmonics.multiReduce(0, {prev, harmonic in
p = phasor(hz * harmonic, sr)
amp = 4 / (harmonic * PI)
out = (sin(p * 2 * PI) * amp) + prev
})
}
}The problem with additive synthesis is that it doesn't scale well. A common technique is to take a single cycle of the band-limited waveform and pre-render it to an array, and play back that single cycle at various speeds. This is called wavetable synthesis.
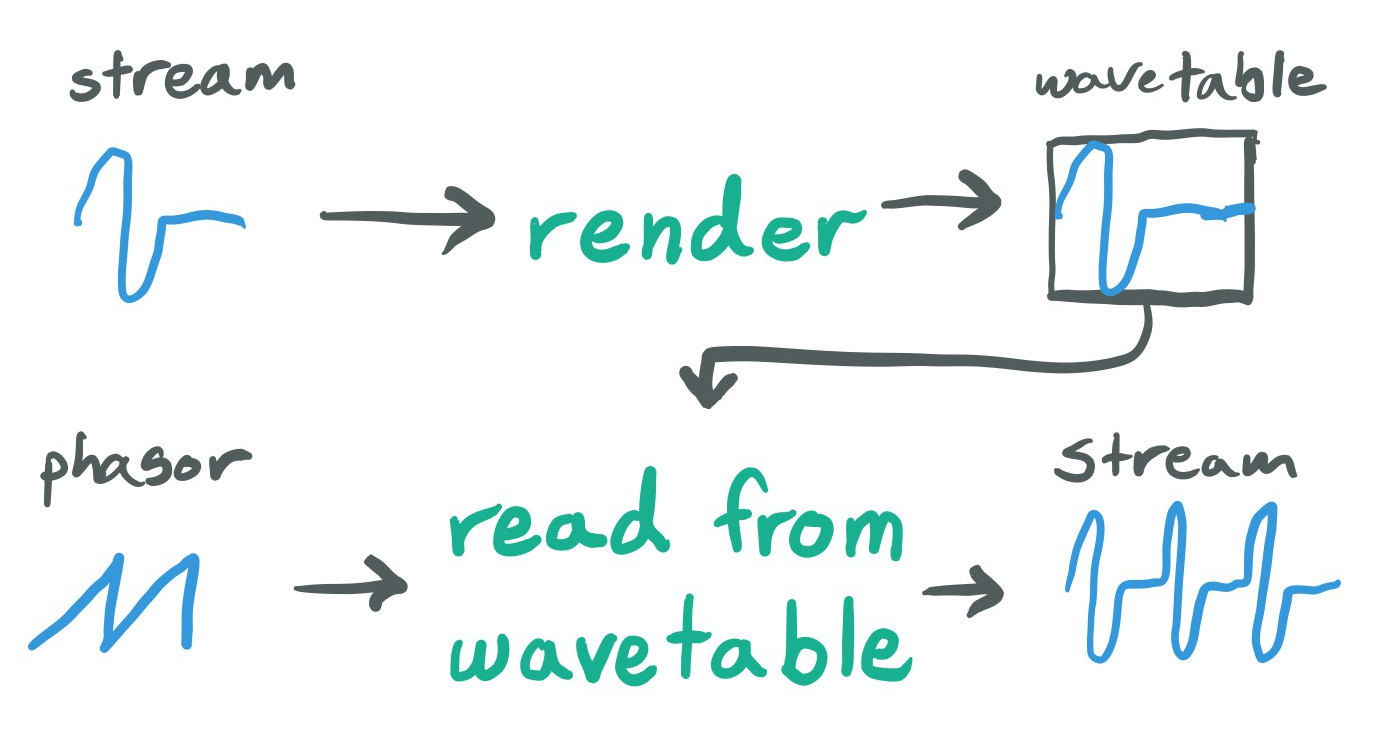
We use two methods, one for creating the wavetable from any synth function we pass in, and another for playing back the wavetable at any speed.
Every synth function we've been using in this example has just two inputs - frequency and sample rate. To render a single cycle with an arbitrary size, we simple set the sample rate to the desired size of the wavetable and set frequency to 1. This makes a single cycle at the right length.
To play back the wavetable we need an interpolation function, which determines what happens when we want to play something in between two individual samples of the wave table.
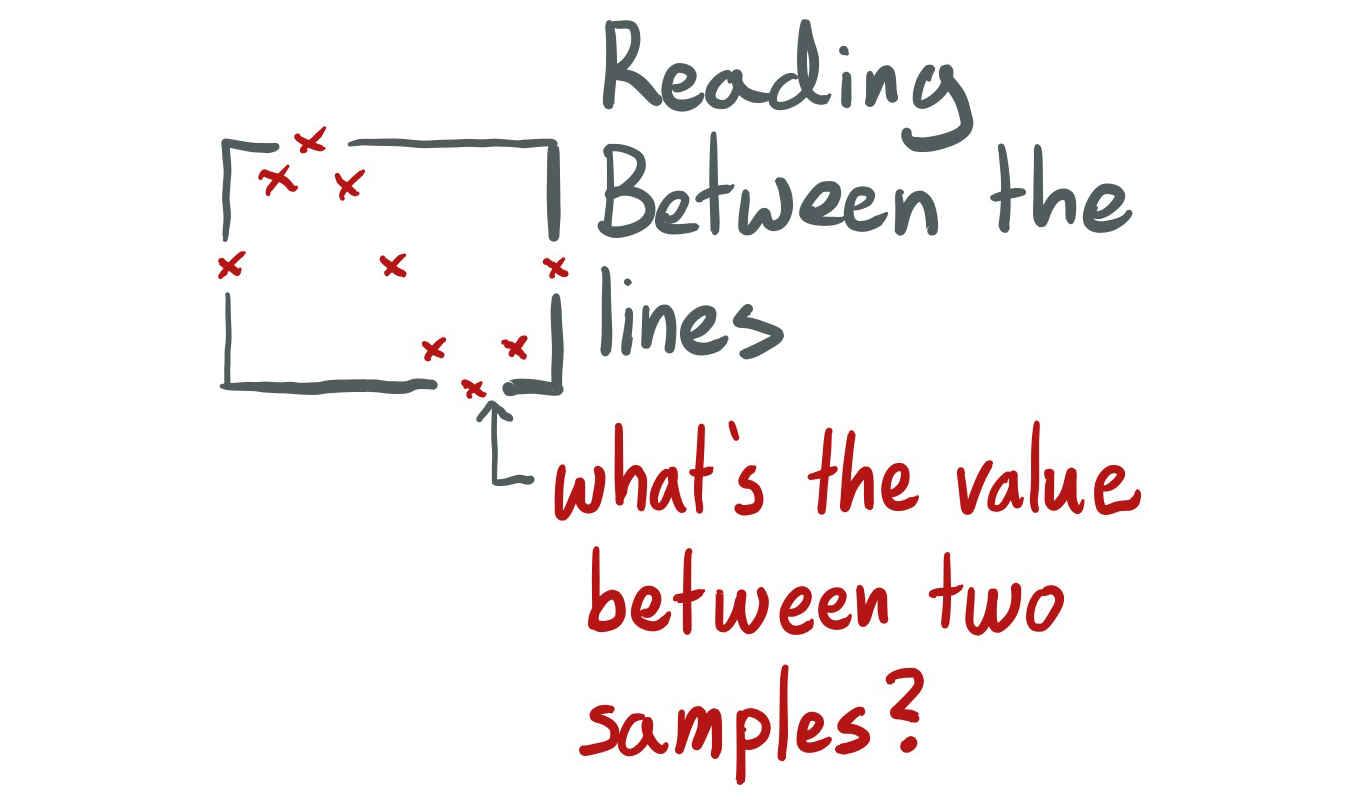
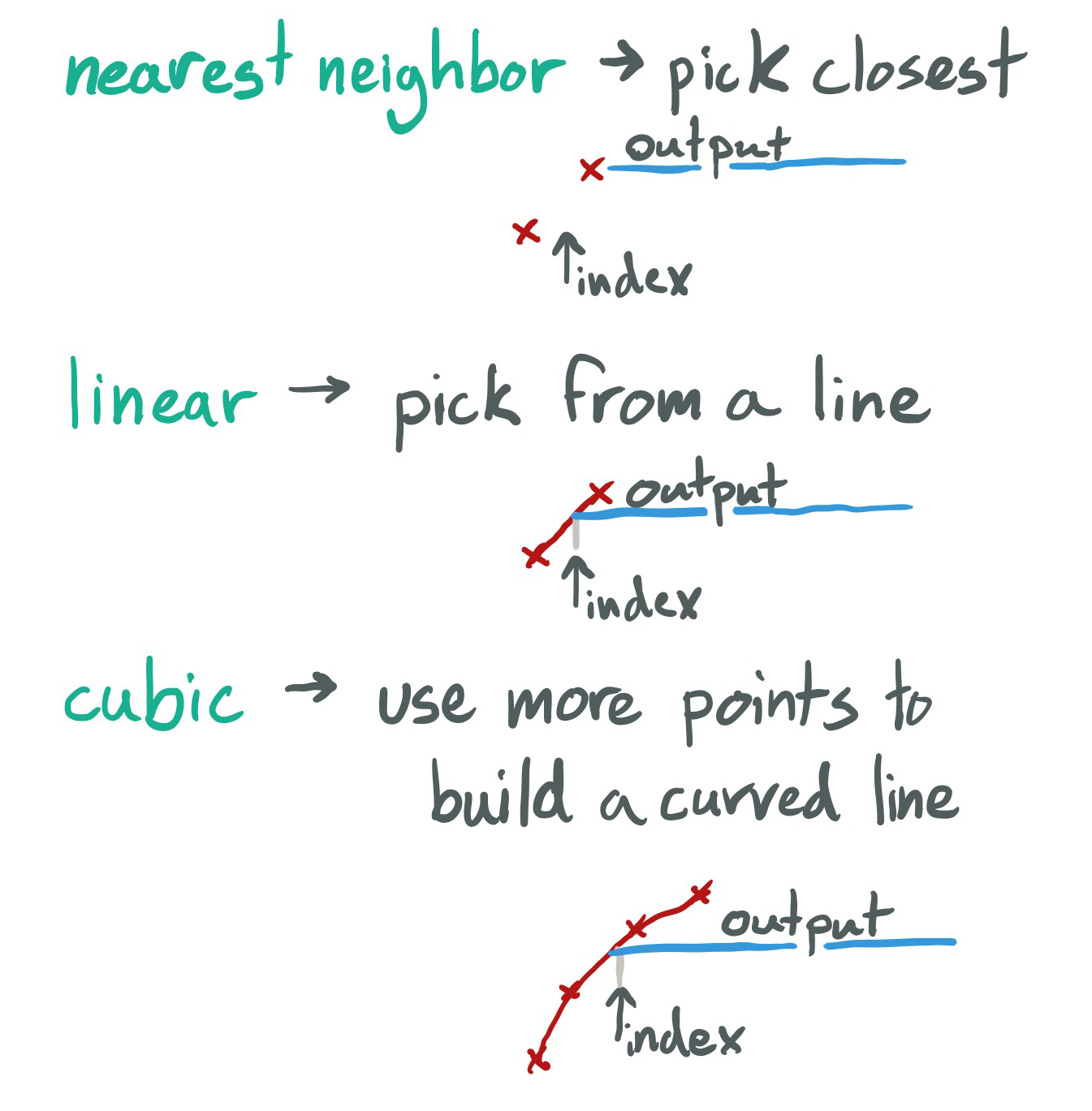
Set synthesisType to wavetableSynthesis in the example and play with the wavetable size and interpolation functions to hear the result.
makeWavetable = {wavetableSize: uint64, func in
wav = func(1, float32(wavetableSize))
out = render(wav, wavetableSize) on init
}
makePlayWavetable = {interpolationFunc, table in
out = {hz, sr in
wavetableSize = len(table)
p = phasor(hz, sr)
iFloat = p * float32(wavetableSize)
out = interpolationFunc(table, iFloat)
}
}There are many other methods for producing anti-aliased waveforms, for example BLEPs, but we'll look at just one more - oversampling. Oversampling reduces frequencies above the Nyquist by simply running at a higher sample rate, filtering everything above the desired Nyquist using a lowpass filter and then converting back to the final sample rate. With this we can use the naive synthesis approach and still limit aliasing.
Set synthesisType to oversampledSynthesis to try it out.
makePlayOversampled = {synthFunc, srMultiplier: uint64 in
out = {hz: float32, sr: float32 in
oversampledSr = sr * float32(srMultiplier)
oversampledStream = synthFunc(hz, oversampledSr)
.rbjLowpass((sr/2) - 2000, 1, oversampledSr)
out = oversampledStream
.render(srMultiplier)
.reduce(0, {x, y in x + y}) / float32(srMultiplier)
}
}
Intonal also has gen streams, which advance whenever referenced, instead of the "once per block tick" rule of normal streams.
main = {
gen i = 1 fby prev + 1
out = i + i + i
}
// Outputs 6 (1 + 2 + 3)These are all the techniques used to control streams. In the future we may introduce one more way - allow advancing streams without referencing them.
There is one more way of controlling flow, mutable values. Whereas streams are treated as immutable (IE they don't change unless advanced), mutable values work more like traditional variables in other languages, except they are only updated on defined events. These are a sort of escape hatch to a more imperative way of dealing with values. In this example, we use it to count the samples in a section.
mutable sectionCountdown = 0
mutate sectionCountdown on sectionAdvance => uint64(beatDurInSamples * curSectionLen)
mutate sectionCountdown on sectionCountdown > 0 => sectionCountdown - 1
sectionAdvance = sectionCountdown == 0
sectionNumIdx = 0 fby ((prev + 1) % len(sectionNums)) on sectionAdvance
curSectionNum = sectionNums[sectionNumIdx]
curSection = sections[curSectionNum]
curSectionLen = curSection.sectionDataLen()
The reason why we use mutable here is the length of the countdown depends on the current section length, which depends on the section index, which depends on the section advance, which depends on the countdown. This is a circular loop which can't be defined with regular streams.
Now you should have a good understanding of how control flow works in Intonal. As always hop on our Discord channel to ask questions or chat! Our final tutorial is coming soon, which will cover bag to create polyphony/multiple objects with independent lifespans.